Completely Randomized Single Factor Experiment Case Study
The project Concept Test.Q, which is by default installed on your computer at C:\Program Files\Q\Examples, contains data from a completely randomized single factor in which four samples of respondents were each shown a different concept for a new yogurt and were asked:
Q4. How likely would you be to buy this product? I would definitely buy it I would probably buy it I am not sure whether I would buy it or not I would probably not buy it I would definitely not buy it
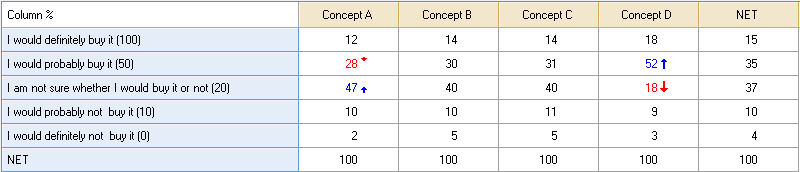
Q4 is a Pick One question. Another Pick One question in the project called Concept indicates which concept was seen by which respondent. The most straightforward way to analyze such data is as a crosstab. The table below shows this crosstab, revealing that Concept D was most popular, with more people saying they would “definitely” buy it and many more people saying they would “probably” buy it.
A second way to analyze the question is to treat Q4 as a Number question, assigning some values to the different categories. The table below shows such an analysis, where “definitely” has been given a Value of 100, “probably” 50, etc. This analysis also shows that Concept D is the most appealing concept and is significantly more appealing than the average of the other concepts. Similarly, it shows that Concept A is least appealing, although we can see from the z-Statistic that Concept A is only marginally less appealing than Concept B and C.
As with all analyses, by default, Q applies the False Discovery Rate Correction to control Type 1 error when determining which cells in the table to indicate as being statistically significant (by color-coding or arrows, depending on the options set for the Table Styles in Project Options). This means that a coefficient that is only just significant at the 0.05 level (e.g., with a z-statistic of more than 1.96 or less than -1.96) will often not be shown as significant. For example, we can see in this example that Concept C has a p-value of 0.0469, but is not shaded as being statistically significant. By setting the Multiple Comparisons Correction to None in Project Options > Statistical Assumptions, these tests can be conducted in the more common way.
In Q, this experiment is considered to have the following properties:
- It has a single task. That is, the respondent was only presented with one set of alternatives (where in this instance, the set contained a single alternative).
- It has a single alternative. That is, the task contains a single alternative. In other words each respondent was only shown one thing, where the thing is called an alternative.
- It has only a single factor. That is, there is only a single attribute (or dimension) which describes the differences between the alternatives. In this case, the attribute contains four attribute levels (i.e., the four concepts).
- The dependent variable (also known as response variable and outcome measure) is numeric.
As with all other types of questions, an Experiment is setup in the Variables and Questions tab by selecting relevant variables, right-clicking and selecting Set Question. The data for this completely randomized single factor experiment is set up in two variables: a variable containing the ratings and a variable containing the attribute:
The dependent variable, with name Q4_3, has a Variable Type of Numeric, which means that the conditional density is assumed to be normally distributed (this is the same assumption as linear regression and ANOVA). The other studies illustrate other types of dependent variables.
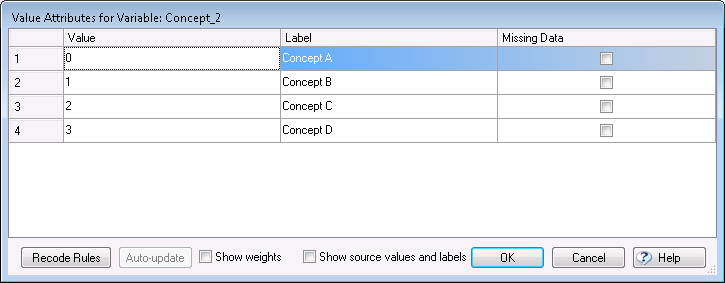
The attribute, which has the name Concept, is contained in the second variable. By pressing the Values button to view the variable’s Value Attributes we see that this variable (and thus the attribute) contains four levels:
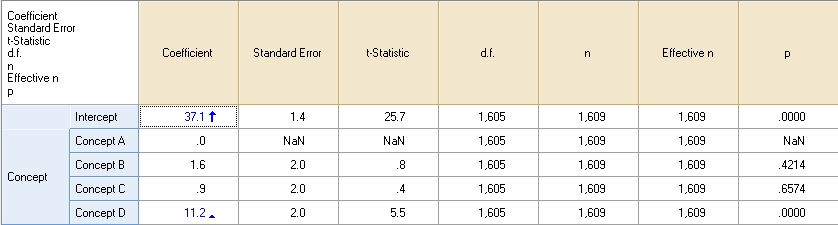
The table below shows the results obtained by Single attribute split cell experiment in the Blue Drop-down menu in the Outputs Tab and selecting the additional statistics by right-clicking on the table, selecting Statistics – Cells, holding Ctrl down and clicking on the desired statistics.
Although at first glance these results appear different to those shown above in the table that contains averages, they are equivalent. The average rating for each concept can be reconstructed by adding their Coefficient to the Intercept (for example, Concept A’s score is 37.1 + 0.0 and Concept B’s score is 37.1 + 1.6). Note that the first concept has been assigned a coefficient of 0 and all other concepts’ coefficients are indexed relative to this 0; the automatic significance tests compare each attribute level (i.e., the concepts in this instance) to the base level. Whichever level is shown first in an attribute is the base level; you can move these around by clicking on them on the Outputs Tab and dragging them. Similarly, you can drag and drop categories to merge them.
Detailed diagnostics can be obtained by selecting all the coefficients and pressing ![]() . The first section of the diagnostics shows the sample size and any filters and weights:
. The first section of the diagnostics shows the sample size and any filters and weights:
Total sample Unweighted base n = 1609
Q automatically conducts a likelihood ratio chi-square test, which essentially checks that the data is not completely random; if the null hypothesis is not rejected, it almost certainly means that there is some error in the way the data has been set up.
Likelihood Ratio Chi-Square Test Chi-Square = 38.872 Degrees of Freedom = 4 Fox, John (1997): Applied Regression Analysis, Linear Models, And Related Methods, Sage. p < 0.000001 Null hypothesis: In the population, all the coefficients are equal to 0. At the 0.05 level of significance, the null hypothesis is rejected.
The Data Summary shows key aspects of the design of the experiment. First, it shows the number of tasks per respondent. In this example, each respondent completed only a single task. Second, it shows the number of alternatives per task. Third, it shows the total number of unique alternatives in the experiment; in this example, there were four unique alternatives (i.e., the first concept), which equated to 0.0025 per task (i.e., 4 unique alternatives divided by 1 * 1,609, where 1 is the number of tasks per respondent and 1,609 the number of respondents). Fourth, it shows the number of unique tasks, which in this instance is also 4. Lastly, it shows the number of unique response patterns, where a response pattern is defined as a task together with a response to the task. In this example, there were five possible answers per task, and four unique tasks. Therefore there were 20 possible unique response patterns. In the data all 20 of these patterns were present, leading to 20 unique response patterns.
Data summary 1 task(s) per respondent 1 alternative(s) per task 4 unique alternatives; 0.00248601615910503 per task 4 unique tasks; 0.00248601615910503 per task 20 unique response patterns
The The Invalid task report identifies any instances where missing or invalid data has caused the exclusion of data from the analysis. In general, this section of the report should appear blank (as in this example), unless different respondents have been asked to complete different numbers of tasks.
Invalid task report Respondent row number (task number)
The Model results present various statistics for the model as a whole and the model’s parameters.
Model results
Dependent Question Type: Number (numeric)
log-likelihood -7,692.330
Null log-likelihood -7,711.766
Parameters 4.000
Effective n 1,609.000
p .000
R-Squared (McFadden) .003
Adjusted R-Squared (McFadden) .002
R-Squared .024
AIC 15,392.661
AIC3 15,396.661
BIC 15,414.194
CAIC 15,414.197
BIC(case) 15,414.194
CAIC(case) 15,414.197
D-Error .000
Parameters
Coef S.E. t-Stat p-Value Beta VIF
Intercept 37.06467662 1.44036180 25.73289336 .00000100 NaN NaN
Concept B 1.63311208 2.03071348 .80420606 .42139708 .02431752 1.50338735
Concept C .90524820 2.04080451 .44357418 .65741026 .01339062 1.49842769
Concept D 11.18968747 2.03824873 5.48985376 .00000005 .16579729 1.49968616