Discrete Choice Experiment Case Study

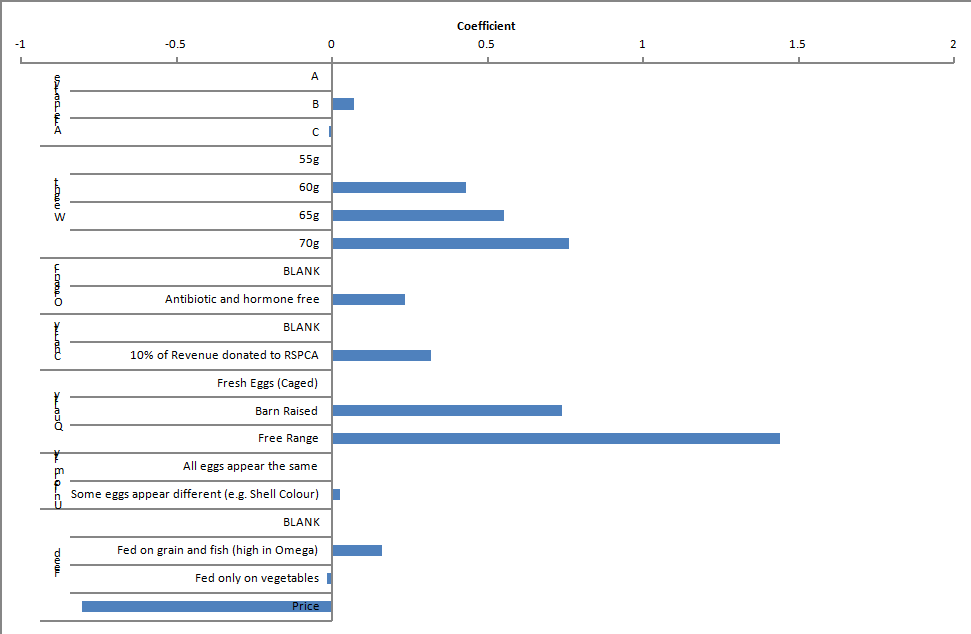
The project Eggs.Q, which is by default installed on your computer at C:\Program Files\Q\Examples, contains a question called Choice-based Conjoint, from an experiment involving eight tasks. The answers to the eight tasks are shown in rows 13 to 20; each has the Label of Choices. Each has Variable Type of Categorical. The attributes for the experiment are shown below.

The Brand Price Trade-Off Experiment was a Labeled choice experiment, where each column (i.e., each alternative) of the question had a “label” (i.e., the brand). The eggs study is an unlabeled experiment, where the columns have no intrinsic meaning. Nevertheless, with an unlabeled experiment we can still estimate parameters (i.e., coefficients) for each of the columns (alternatives) in a choice task; these are commonly referred to as alternative specific constants and their construction is shown in variables 21 to 44 in the example project.

Attribute	Level 1	Level 2	Level 3	Level 4
Weight	Average Egg Weighs 55g	Average Egg Weights 60g	Average Egg Weights 65g	Average Egg Weights 70g
Organic	BLANK [nothing shown]	Antibiotic and hormone free
Charity	BLANK [nothing shown]	10% of Revenue donated to RSPCA
Quality	Fresh Eggs (Caged)	Barn Raised	Free Range
Uniformity	All eggs appear the same	Some eggs appear different (e.g., shell colour)
Feed	BLANK [nothing shown]	Fed on grain and fish (high in Omega)	Fed on vegetables
Price	Range of price points from $3.35 to $6.50

By selecting all the cells and pressing we can obtain standard diagnostics for the model. One of the diagnostics that can be obtained is the AIC, which is a useful way of comparing alternative specifications of a discrete choice experiment. For example, the eggs experiment’s AIC is 5,879.048.

There are a variety of different ways of modifying an Experiment. The simplest is to change a categorical attribute into a numeric variable or vice versa. For example, consider the Weight attribute. As shown above, the utility that the consumers attach to weight appears non-linear. That is, there is a large jump from 55g to 60g (where 55g is the benchmark level with a utility of 0), and much smaller increments between the remaining egg weights. If this pattern is reflective of the real-world, it is something of an insight (i.e., it means that it is quite important for a manufacturer to offer 60g eggs, but of less incremental benefit to offer yet heavier eggs). An alternative explanation for the pattern is that it is sampling error; we can test this alternative assumption by comparing this model shown in the chart with an alternative model where egg weight is treated as a numeric attribute.

If we right-click on the Weight attribute and select Convert to Numeric Attribute, Q re-estimates the model with the attribute treated as being numeric. Right-click again and select Values… to see the Value Attributes dialog box. This shows us that the Value for the categories are 0, 1, 2 and 3; to recode them (and have the model re-estimated using the recoded values), change these values to represent the weight in 10s of grams (5.5, 6.0, 6.5 and 7.0). Again select all the cells and press to assess the model fit; the AIC is now 5,883.488, which is higher than the earlier AIC. The way that the AIC works is that the lower the value, the greater the evidence in favor of the model. In this case, this tells us that we should not treat egg weight as being a numeric attribute and can instead draw valid inferences from any non-linear patterns that are evident. To convert the attribute back to categorical, right-click yet again on Weight and select Convert to Categorical Attribute.

The advantage of modeling as categorical is that non-linear relationships may be identified. The advantage of modeling as numeric (i.e., linear) is that noise from the survey is smoothed out. This benefit of modeling as linear is most evident when modeling interactions.

It is possible to employ monotonicity constraints, which enforce that the coefficients of a particular attribute level are ordered from lowest to highest (in accordance with the Value of the variable). This is done by changing the Variable Type to Ordered Categorical (selecting all the variables of the attribute in the Variables and Questions tab. This should be done with some caution, as it can cause an irrelevant variable to appear more important than it is. For example, if an attribute was truly irrelevant to people, random noise will guarantee that some people’s data will show a positive effect and others a negative effect; employing the monotonicity constraints causes the negative effect to be ignored, leaving only the positive effect. As a consequence, using monotonicity constraints can cause the models to become less accurate predictors of market behavior. For this reason, monotonicity constraints are often only appropriate with very small sample sizes or very large numbers of segments. Significance tests and standard errors may be inaccurate when monotonicity constraints are employed. The constraints are ignored if estimating Multivariate Normal – Full Covariance (specified in Distributions).

Additional examples of choice experiments are provided in the next page.

Next

• Conjoint Analysis Case Study

See also

• Experiments
• Experiments Specifications
• Completely Randomized Single Factor Experiment Case Study
• Brand Price Trade-Off Experiment
• MaxDiff Case Study
• Individual-Level Parameters

Notes

Template:Reflist