Principal Components Analysis
Principal Components Analysis identifies interrelationships between variables. It is useful for identifying underlying dimensions of consumer behavior, summarizing data and identifying redundant questions in questionnaires.
PCA
In Q5 and later versions the best approach to PCA is Create > Dimension Reduction > Principal Components Analysis. This option uses R (![]() ).
).
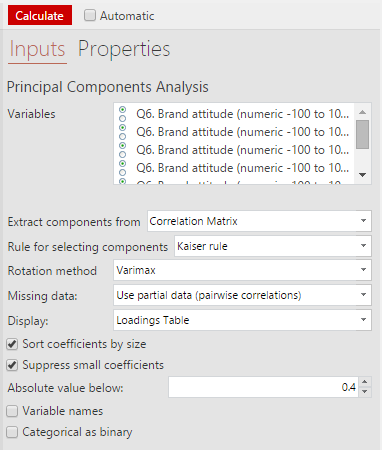
Selecting this option will add a new output to your Report. When you select this item, the options for the analysis will be shown on the right-hand side of the screen in the Object Inspector. For details about the options, see Dimension Reduction - Principal Components Analysis.
The workflow to using this item is as follows:
- Click into the Variables box and tick the variables you want to include in the analysis
- Change any of the options as desired
- Click Calculate
The resulting Loadings Table output will show you columns for each component that has been identified, and the loading for each of the input variables.
Data Setup
For most applications, the variables that you select in the PCA should be numeric. That is, you should change the Question Type of question(s) containing the variables that you want to use to Number or Number - Multi before running the analysis. This ensures that the analysis runs based on the underlying values rather than on any categories. The variables that you select for the analysis do not need to belong to the same question - they can come from two or more different questions.
Saving Scores as Variables
Once you are happy with the analysis, you can save variables corresponding to the principal components into your data set. To do so, select the PCA output in your report and then select Create > Dimension Reduction > Save Variable(s) > Components/Dimensions. A new Number - Multi question will be added to the data set.
The new variables are linked back to your PCA output. If you change an option and calculate the PCA again, the scores will also update. If you change the number of components in the analysis, you should delete the variables for the scores in the Variables and Questions tab and save a new set of scores.
Legacy PCA
| Related Online Training modules | |
|---|---|
| Principal Components Analysis | |
| Generally it is best to access online training from within Q by selecting Help > Online Training |
Prior to Q5, the principal components analysis option worked differently. The old option is still available in Q5 as Legacy PCA. It is not as flexible as the option described above, particularly with regard to missing data. Cases with any missing values in any of the variables will be excluded from the analysis. That is, this analysis can only include respondents who have complete data.
The legacy principal components analysis (PCA) is run in Q by:
- Select the question you wish to analyze in the Blue Drop-down Menu. If there are multiple questions, you will need to first combine them into a single question.
- Change the question's Question Type to Number - Multi (Q will also analyze a Pick Any question, but you will find the outputs harder to interpret).
- Select Create > Dimension Reduction > Legacy PCA to run a principal components analysis (PCA).
Buttons, options and fields
Principal components analysis is a technique which turns a set of numeric variables into another, smaller, set of numeric variables.
Rule for selecting components
- Kaiser rule Selects components with eigenvalues greater than or equal to 1.
- Broken stick Selects components with eigenvalues greater than predicted by a broken stick distribution.
- Eigenvalues over Specify a cutoff point for retaining eigenvalues.
Number of components Retains this number of components (the largest components are retained).
Varimax Performs a Varimax rotation of the components (and loadings) to facilitate interpretation.
Ignore NET and SUM Excludes the NET or SUM row from the analysis.
See also
- SurveyAnalysis.org for an overview of Principal Components Analysis.