Anchored MaxDiff
Anchored MaxDiff experiments supplement standard MaxDiff questions with additional questions designed to work out the absolute importance of the attributes. That is, while a traditional MaxDiff experiment identifies the relative importance of the attributes, an anchored MaxDiff experiment permits conclusions about whether specific attributes are actually important or not important.
Examples
These examples are from the data contained in File:AnchoredMaxDiff.QPack.
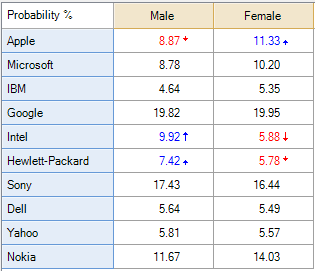
The table on the left shows the Probability % from a traditional MaxDiff experiment in which the attributes being compared are technology brands. Looking at the analysis we we can see that:
- Google and Sony come in first and second place in terms of preference.
- Apple has done better amongst the women than the men.
- Intel and HP have done relatively better amongst the men than the women.
If you add up the percentages, each column adds to 100% and thus the analysis only focuses on relative preferences. Thus, while a naive read of the data would lead one to conclude that women like Apple more than do men, the data does not actually tell us this (i.e., it is possible that the men like every single brand more than do the women, but because the analysis is expressed as a percentage, such a conclusion cannot be obtained).
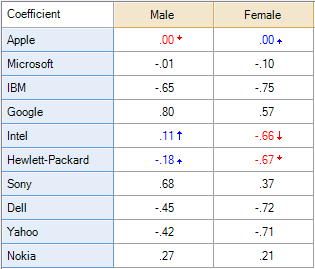
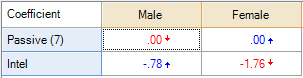
The table on the right shows the same analysis but in terms of the Coefficient. This is also uninformative, as these are indexed relative to the first brand, which is Apple. Thus, that men and women both have a score of 0 is an assumption of the analysis rather than an insight (the color-coding is because the significance test is comparing the relativities, and 0 is a relatively high score for the women).
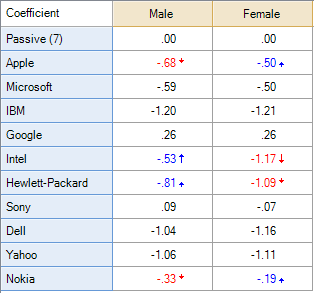
Anchored MaxDiff resolves this conundrum by using additional data as a benchmark. In the table below, a question asking likelihood to recommend each of the brands has been used to anchor the MaxDiff experiment. In particular, a rating of 7 out of 10 by respondents has been used as a benchmark and assigned a coefficient of 0.[note 1] All of the other coefficients are thus interpreted relative to this benchmark value. Thus, we can see that Apple has received a score of less than seven amongst both men and women and so, in some absolute sense, the brand can be seen as performing poorly (as a score of less than seven in a question asking about likelihood to recommend is typically regarded as a poor score). The analysis also shows that men have a marginally lower absolute score than do women in terms of Apple (-0.68 versus -0.50), whereas Google has equal performance amongst the men and the women.
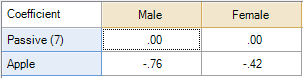
The significance tests indicated by the color-coding are showing relative performance. Thus, if we wish to test whether the difference between Apple by gender is significant we need to remove all the other brands from the analysis. This is shown on the left. The table on the right only contains the data for Intel; it shows that Intel is significantly more preferred, in an absolute sense, amongst men than women.
The two analyses above were created by selecting rows to remove, right-clicking and selecting Remove, and putting the brands back in again by right-clicking and selecting Revert. In each case, the automatic significance testing focuses on relativities.[note 2] To see how the brands perform in an absolute sense, we need to use gender as a filter rather than as the columns (as when using gender in the columns Q interprets this as meaning you are wanting to compare the genders).
The table output below shows the table with a Filter for women and with a Planned Test of Statistical Significance explicitly comparing Apple with the benchmark value of 0, which reveals that the absolute performance of Apple amongst women is significantly below the benchmark rating of 7 out of 10.
Types of anchored MaxDiff experiments
There are two common types of anchored MaxDiff experiments.
Dual response format
The dual response format involves following each MaxDiff question with another question asking something like:
Considering the four features shown above, would you say that... ○ All are important ○ Some are important, some are not ○ None of these are important.
MaxDiff combined with rating scales
Before or after the MaxDiff experiment, the respondent provides traditional ratings (e.g., rates all the attributes on a scale from 0 to 10).
The logic of standard MaxDiff analysis in Q
In order to understand how to set up MaxDiff experiments in Q it is necessary to first understand how Q interprets MaxDiff data. Q interprets each MaxDiff question as a partial ranking. Thus, if a respondent was given a question showing options A, B, C and F, and chose B as most preferred and F as least preferred, Q interprets this as the following ranking: B > A = C > F. Note that this is a different model to that used by Sawtooth Software.[note 3]
As discussed in MaxDiff Specifications, when each of the choice questions is set up in Q a 1 is used for the most preferred item, a -1 for the least preferred item, 0 for the other items that were shown but not chosen and NaN for the items not shown. Thus, B > A = C > D is encoded as:
A B C D E F 0 1 0 NaN NaN -1
where the alternatives not shown are coded as NaN.
Note that when analyzing this data Q only looks at the relative ordering and any other values could be used instead, provided that they imply the same ordering.
Setting up anchored MaxDiff experiments in Q
Setting up the dual response format anchored MaxDiff studies in Q
Anchoring is accommodated in Q by introducing a new alternative for each choice question. In the case of the dual response, we will call this new alternative Zero. Consider again the situation where the respondent has been faced with a choice of A, B, C and F and has chosen B as best and F as worst, which leads to B > A = C > F.
The Zero alternative is always assigned a value of 0. The value assigned to the other alternatives is then relative to this zero value.
All are important
Where all of the items are important this implies that all are ranked higher than the Zero option:
A B C D E F Zero 2 3 2 NaN NaN 1 0
Some are important
Where some of the items are important this implies that the most preferred item must be more important than Zero, the least preferred item must be less preferred than Zero, but we do not know the relative preference of the remaining items relative to Zero, and thus this is coded as:
A B C D E F Zero 0 1 0 NaN NaN -1 0
Note that although this coding implies that A = C = Zero, the underlying algorithm does not explicitly assume these things are equal. Rather, it simply treats this particular set of data as not providing any evidence about the relative ordering of these alternatives.
None are important
A B C D E F Zero -2 -1 -2 NaN NaN -3 0
Practical process for setting the dual response variables in Q
Ultimately, new variables need to be created that combine the MaxDiff data with the dual response anchoring data for each MaxDiff task. Many MaxDiff data formats store the responses as one best and one worst variable per MaxDiff task. To accommodate the dual response anchor data, these best/worst variables must be restructured into one variable per option, per task.
This means that using the example above where the MaxDiff has 6 options, A-F, with 4 exposed per task, the two best/worst variables per task become 7; one new variable per option, along with Zero. In a 4 task MaxDiff, this means that the 4 best and 4 worst variables become 28 new variables. These new variables must be manually created either within Q or created externally and added into the Q project by merging data files.
Here's an example of how to work through creating these new variables:
Respondent 1's first task has alternatives A, B, C, F. The best choice for Respondent 1, task 1 is B, with a value of 2, and the worst choice for Respondent 1, task 1 is F with a value of 6, therefore best is alternative 2 and worst is alternative 6. The dual response anchor variable for respondent 1, task 1 is "1", indicating that all alternatives are important.
Task1_best Task1_Worst Anchor
2 6 1
The new variables created from combining the MaxDiff responses with the anchor data using the logic outlined above look like this:
task1alt1 task1alt2 task1alt3 task1alt4 task1alt5 task1alt6 task1zero
2 3 2 NaN Nan 1 0
Alternative 2 (B) is assigned 3 because it is the best, alternatives 1 (A) and 3 (C) are assigned 2 because they were seen in the task, not as preferred as alternative 2 but better than the worst alternative which is alternative 7 (F), which is assigned 1. Since they are all preferred (Anchor = 1), they are greater than 0. The Zero alternative must be included for each task and is always assigned 0. Any alternatives that did not appear in the task are assigned NaN.
If instead, the MaxDiff data is the same, but the anchor value is 2 so "Only some" of the alternatives are important, we interpret that to mean that the best (alternative 2) is greater than 0, the worst (alternative 7) as less than 0, and the other alternatives that are not selected are 0. Then the data would instead look like:
task1alt1 task1alt2 task1alt3 task1alt4 task1alt5 task1alt6 task1zero
0 1 0 NaN Nan -1 0
Finally, if the anchor value is 3, meaning none of the alternatives are important to the respondent, then all of the values fall below zero, with the most important closest to zero, and the least important furthest from zero:
task1alt1 task1alt2 task1alt3 task1alt4 task1alt5 task1alt6 task1zero -2 -1 -2 NaN Nan -3 0
You would then create a new set of variables for each task, then append them to your data set. Combine them into a Ranking question and from there you can use it in the MaxDiff analysis.
Setting up the combined MaxDiff with ratings in Q
Prior to explaining how to use ratings to anchor the MaxDiff it is useful to first understand how ratings data can be combined with the MaxDiff experiment without anchoring. Again the situation where a MaxDiff task reveals that B > A = C > F. Consider a rating question where the six alternatives are rated, respectively, 9, 10, 7, 7, 7, 7 and 3. Thus, the ratings imply that: B > A > C = D = E > F and this information can be incorporated into Q as if just another question in the MaxDiff experiment:
A B C D E F 9 10 7 7 7 3
Anchoring is achieved by using the scale points. We can use some or all of the scale points as anchors.[note 4] From an interpretation perspective it is usually most straightforward to choose a specific point as the anchor value. For example, consider the case where we decide to use a rating of 7 as the anchor point. We create a new alternative for the analysis which we will call Seven.
In the case of the MaxDiff tasks, as they only focus on relativities, they are set up in the standard way. Thus, where a MaxDiff question reveals that B > A > C = D = E > F, we include this new anchoring alternative, but it is assigned a value of NaN as nothing is learned about its relative appeal from this task.
A B C D E F Seven 0 1 0 NaN NaN -1 NaN
The setup of the ratings data is then straightforward. It is just the actual ratings provided by respondents, but with an additional item containing the benchmark value:
A B C D E F Seven 9 10 7 7 7 3 7
Notes
Further reading: MaxDiff software
Cite error: <ref> tags exist for a group named "note", but no corresponding <references group="note"/> tag was found