Latent Class Analysis

Related Online Training modules
	Latent Class Analysis with Categorical and Numeric Data
	Latent Class Choice Model
	Latent Class Analysis with Categorical Data
	Latent Class Analysis with Numeric Data
	Latent Class Analysis with Ranking Data
	Individual-Level Parameters
	Generally it is best to access online training from within Q by selecting Help > Online Training

Latent class analysis is a statistical technique for grouping together similar observations (i.e., creating segments).

How to run Latent Class Analysis in Q

The first step depends on which version of Q you are using:
- Q5.0 and later: Create > Segments > Latent Class Analysis
- Older versions of Q: Create > Segments
Select the questions to be used to form the segments in the Questions to analyze dialog box.
If necessary, modify the default options. Note that:

By default Q will automatically select the number of segments using the Bayesian information criterion. You can alternatively specify a specific number of segments by selecting the Manual option. Alternatively, you can select a different information criteria by clicking Advanced.
The Question Type of the questions that are analyzed determines how the latent class model is conducted. For example, when analyzing a Pick One - Multi any scale points are ignored and Q treats the data as categorical; if it is converted to a Ranking Q focuses on understanding relativities; if it is converted to Number - Multi Q treats the data as being numeric. Note, a Pick Any question with a Categorical Variable Type vs a Numeric Variable Type will be treated the same in the model.

Technical outputs

There are two main sets of outputs from a latent class analysis. The main output is the 'tree', which is discussed in the next major section on this page. However, prior to showing you the tree, Q shows you more technical outputs in the Grow Settings and Analysis Report. These outputs are discussed here. These outputs can also be obtained by right-clicking on the 'tree' and selecting Grow Settings and Analysis Report.

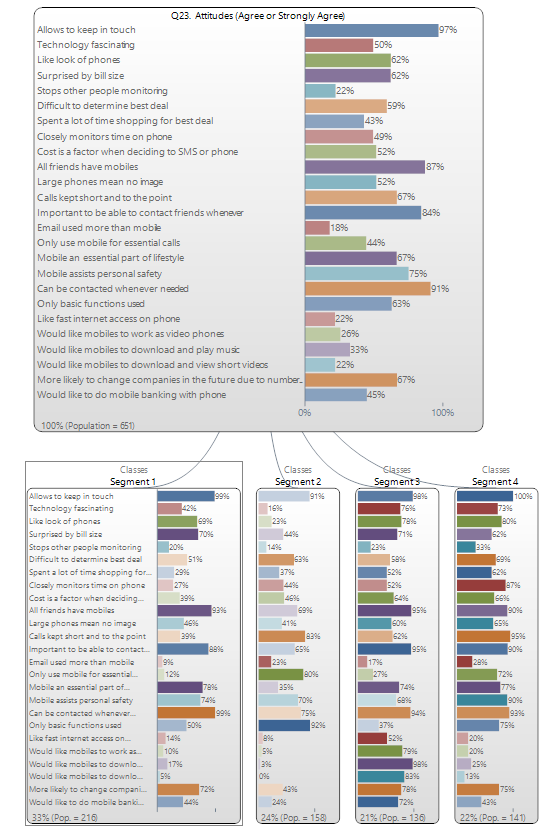
The outputs described below have been created from a latent class analysis of Q23. Attitudes (categories) in Phone Tidied.Q, which is by default installed on your computer at C:\Program Files\Q\Examples.

Grow Settings

This shows the various technical assumptions that have been used when conducting the latent class analysis. For example:

Automatic number of segments, 1 - 10
Objective: Mixture
Model selection criterion: BIC
Minimum node size to split: 25
Maximum number of tree levels: 2
Iterations: 1000
Starting values: 
Number of starts: 1
Initial classification: (none)
Number of draws: 100
Draw generation method: Halton
Question-specific assumptions:
Question                     Weight   Distribution   Pool variance 
Q23. Attitudes (categories)    1         Finite          No

Number of Responses

This indicates the amount of observations. It can differ by question. See Missing Values in Latent Class Analysis.

Convergence data

This shows whether or not each model estimated converged. For example, the following output shows that models with 1 through 4 classes all converged. 'Converged' means that the model estimated; if a model does not converge it means that Q was unable to reach the correct solution with the assumptions specified; most commonly increasing the maximum number of Iterations in Advanced can result in convergence.

1 classes: Converged
2 classes: Converged
3 classes: Converged
4 classes: Converged

Fit statistics

This is a table showing the diagnostics used to determine the number of classes, as well as some related statistics.

           Log-likelihood  Parameters         BIC  R-Squared  Entropy  Iterations
Aggregate     -22,708.404     100.000  46,064.660       .000      NaN       2.000
2 classes     -21,833.966     201.000  44,970.113       .039     .899      49.000
3 classes     -21,389.218     302.000  44,734.945       .058     .904      84.000
4 classes     -21,212.304     403.000  45,035.446       .066     .932     301.000

3 class solution has the best (lowest) BIC

The BIC is the default information criteria used with latent class analysis. In this case it suggests a 3 class solution. The BIC is a very rough guide to the appropriate number of classes – it is often appropriate to have a different number of classes to that recommended by the BIC. The BIC statistic cannot be used to compare solutions with different data or identified with Objective as Clustering with solutions identified using other methods.

The BIC takes into account weights in two ways. First, the weights, which are modified to sum to the effective sample size, are reflected in the log-likelihood. Second, the effective sample size is used in the penalty when computing the BIC.

In this example, because the 4 class solution was worse than the 3 class solution Q did not evaluate any larger solutions.

The R-Squared statistic^{[note 1]} should not be interpreted in the way that is common with regression models. The more variables in a model, the lower the R-Squared. For example, an R-Squared of 0.10 could be from a valid and useful model. It is not displayed where numeric variables are used.

Entropy is a measure of how accurately respondents can be assigned to the classes. A score of 1 indicates that there is 100% certainty about allocation. With scores below 0.8, it is possible to get non-trivial differences between the outputs shown by the latent class analysis (i.e., on the tree, and in fit statistics), and those obtained when crosstabbing the latent class membership variable with the input data. In general, entropy is not so useful when comparing alternative numbers of segments, and its main role is in working out whether there will be inconsistencies between the results on the tree and fit statistics, and those obtained from crosstabs. When entropy is poor, it is usually best to only rely on crosstabs when comparing segmentations.

Iterations shows how long the algorithm took to compute. By default the algorithm stops when the number of iterations is 1,000. If this is observed, the number of iterations should be increased. Other than for this purpose, the number of iterations is not a useful diagnostic for latent class analysis.

Class Sizes, Class Parameters and Individual-level parameter shrinkage

These outputs are generally not useful for model-based clustering applications of latent class analysis, such as the one being described above. Please refer to the MaxDiff Case Study for a discussion of these parameters.

The 'tree'

The following 'tree' has been created using Q23. Attitudes (Agree or Strongly Agree) in Phone Tidied.Q, which is by default installed on your computer at C:\Program Files\Q\Examples. As the (upside-down) 'tree' has four 'branches' we can see that four segments have been identified. The blob at the top of the tree shows the results for the total market. Each of the four blobs underneath show the results for different segments, with the size of the segments shown at the bottom.

Note that if you change the Distribution settings, and create a model with only a single segment, the results shown in the tree will be different to those shown in the node at the top. The reason for this is that the node on the top shows the results of estimating a single model for the entire sample, whereas the node underneath shows the model for the average person, under the assumption that there is variation in the population, and this variation follows a normal distribution. At an intuitive level it is surprising that these results are different, as in many standard problems in data analysis these two results will be the same. The technical reason that they are not the same is that the underlying models are non-linear, and the two models will only have the same results for linear models. As most people are most familiar with linear models, people tend to get surprised by this seeming contradiction.

Buttons, Options and Fields

Questions to analyze The questions to use to form the classes. Grid questions cannot be selected (you need to first change their Question Type to another type.

Number of segments per split

Automatic Evaluates segments in the specified range, starting with Minimum and finishing when either the Information Criterion increases (see Advanced), or, the Maximum is reached.

Manual The specified Number of classes are created. When creating a tree, Q uses this setting for each split ('branch') of the tree. (You can specify the Maximum number of tree levels and the Minimum node size per split in the Advanced options.

Advanced

Iterations The number of iterations of the estimation algorithms.

Initial classification A question that is used as a starting point for latent class analysis.

Starting values Initial values to be used in the first iteration of the algorithm.

Number of starts Number of times that the latent class algorithm is run for a given number of classes. Cases are randomly allocated to segments each time (a common seed is used to that you will get the same results each time you run it, unless you change the input data.)

Number of draws Number of draws used in computing the simulated likelihood (for Conjoint and Ranking questions with non-Finite distributions).

Draw generation method The method used for pseudo-random generation for computation of the simulated likelihood.

Maximum number of tree levels The maximum size of the tree (the tree may be smaller if the Information Criteria fails to support a split as being appropriate).

Minimum node size to split Nodes on the tree (i.e., segments) are not split if their sample size is smaller than this number.

Objective This setting can be used to make Q mimic the behavior of other data analysis tools (see also Statistical Model for Latent Class Analysis, Mixed-Mode Tree, and Mixed-Mode Cluster Analysis):

Mixture uses a mixture model (e.g., latent class analysis), where units of analysis are assigned to segments probabilistically. This is the standard assumption in modern work on classification and is the setting used as the default in all latent class analysis programs, including Q (when Form segments by is set to splitting by individuals (latent class analysis, cluster analysis, mixture models).

Discrete uses the latent class log-likelihood but assigns units of analysis discretely. For example, if a unit of analysis has a 40% probability of being assigned to class 1 and 30% to class 2 and class 3, the unit of analysis is assigned to class 1 at each stage of the estimation process. This is used in Q when Form segments by is set to splitting by splitting by questions (tree).

Clustering uses the Classification Likelihood, where units of analysis are assigned to one-and-only-one segment and segments are assumed to all be of the same size.

Model selection criterion Rule used to select the number of classes when Number of segments per split is set to Automatic (see Options). Determines which of the Information Criteria is used. The various information criteria that are used are ordered from the one that will create the biggest trees (the AIC) through to the one that will create the smallest trees (CAIC). There is no clear statistical theory to guide the choice of information criteria.

Question-specific assumptions

Weight Modifies the contribution of a particular question in determining the final solution by modifying its weight.

Distribution See Distribution.

Notes

Template:Reflist

Further reading: Latent Class Analysis Software
Cite error: <ref> tags exist for a group named 'note', but no corresponding <references group='note'/> tag was found

[note 1]