Correspondence Analysis
| Related Online Training modules | |
|---|---|
| Correspondence Analysis | |
| Generally it is best to access online training from within Q by selecting Help > Online Training |
Correspondence Analysis below is only available in Q and is conducted using our legacy analyses the Maps dialog box. See Dimension Reduction - Correspondence Analysis of a Table for our updated feature.
Required data
Any table that contains rows and columns, including contingency tables, grids (e.g., from a Pick Any – Grid question) and RAW DATA.
Statistic used in the analysis
Q computes the analysis using whichever of the following statistics is available on the table (where multiple are available, the one that appears first is used):
Interpretation
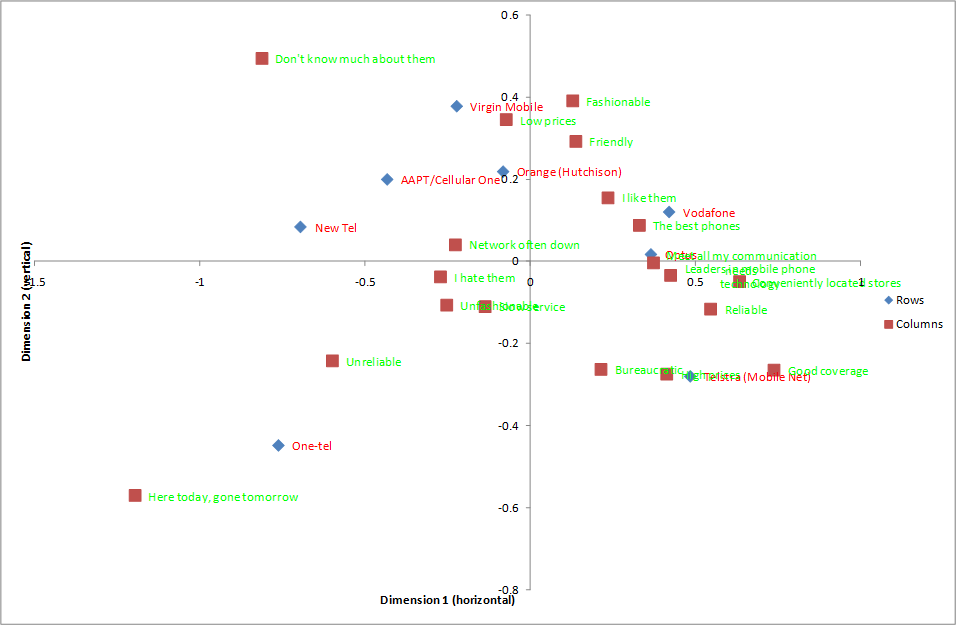
Consider the large image grid shown below (a Pick Any – Grid) question taken from Q20 of Phone 1.Q). The resulting correspondence analysis biplot (scatter plot) is shown below the table.
This correspondence analysis chart quickly allows us to see that One-tel was seen by consumers as being associated with Here today, gone tomorrow (the company was in financial trouble at the time of the study), the new entrants to the market, AAPT and Virgin are shown as Don’t know much about them and the market leader, Telstra (Mobile Net), skews towards Good coverage and Bureaucratic.
Interpreting correspondence analysis chart is not as straightforward as many assume. It is not appropriate to simply draw conclusions by looking at the distance between things on the map. If you understand the interpretation of the principal components biplot, then correspondence analysis can be interpreted as a corrected form of the biplot, with the nature of the correction being that it focuses on relativities (i.e., rather than highlighting which brands scored high on which attributes, correspondence analysis instead highlights which brands scored relatively high on which attributes).
When interpreting a correspondence analysis map, you need to keep the following things in mind:
- Maps show relativities. For example, Telstra (Mobile Net) was Australia’s largest mobile carrier at the time of the study, which means that it has the highest percentages on most of the things shown in the table. As it cannot be shown to be related to every attribute, the correspondence analysis positions Telstra (Mobile Net) by looking only at the relativities in the table (also revealed by the color-coding and arrows in the table).
- The correspondence analysis is based on normalized data. That is, rather than computing positions on the map by looking directly at the data in the image grid, it instead essentially looks at the standardized residuals; that is, the difference between the observed counts and the expected counts. (To get a better idea of the information that the correspondence analysis is relying on, view the z-Statistics using Statistics – Cells; the actual correspondence analysis algorithm does not use these same z-statistics).
- Q charts the principal coordinates of the correspondence analysis. The principal coordinates take into account the inertia of the dimensions (described below). So, if the first dimension is much more important than the second, this will be reflected in how the map has been drawn (i.e., the second dimension’s scale will be small if the dimension is relatively unimportant).
- The aspect ratio of the map needs to be “respected”. That is, the scales of x and y axes outputted into Excel are meaningful in terms of the scale on which the labels are charted and, consequently, it is necessary to manually resize the chart so that the horizontal and vertical distances are equivalent.
- You can compare “similar” objects on the map based on their distances. In the case of traditional correspondence analysis and correspondence analysis of a square matrix, “similar” means that you can compare row categories with each other and column categories with each other. In the case of multiple correspondence analysis, it means that you can compare categories in a variable.
- When comparing non-“similar” categories (i.e., row categories with column categories or categories of different variables), you need to imagine a line from each object to the center of the map and assess the angle at which the two lines meet. If the angle is very small it suggests the row and column labels are associated (and, if they are both far from the center of the map it suggests a relatively strong association). If the angle is a right angle, it suggests no relationship. If the angle is more than 90 degrees, it indicates a negative association. Moon charts are more readily interpretable – see the next section.
- The charts are compressing a large amount of information and this often causes distortions. Most commonly, two things may appear to be associated (i.e., have a small angle between the line that connects each to the origin), but this is because they are both negatively associated with the same things. For example, a sports car and an SUV may be located near each other on map of the car market because they are not sedans. It is always wise to check that any insights garnered from a table are also evident in the data.
Interpretation of technical outputs
The outputs shown in this section are from a correspondence analysis of Preferred Cola by Q3. Age in Cola.Q, where the NET Sugarred and NET Sugarless categories were deleted prior to conducting the analysis. The first outputs show the sample size and the correspondence analysis algorithm used.
Total sample Unweighted base n = 322; total n = 327; 5 missing Correspondence Analysis (Traditional)
Correspondence analysis assumes that numeric factors underlie the categorical data. The Canonical Correlation shows the correlation between the different questions (or rows and columns) within each dimension. For example, if Preferred Cola and Q3. Age have their Question Type changed from Pick One to Number, with their values recoded to the principal coordinates of the first dimension (i.e., the position on the map on the x-axis), the correlation between the questions is 0.279. The Inertia is the squared canonical correlation. The Proportion is the Inertia divided by the sum of the inertias. In this example, 38.5% of the inertia is in the first dimension and 28.2% in the second dimension, meaning that the map show 67% of the patterns (38.5% + 28.2%).
Inertia(s):
Canonical Correlation Inertia Proportion
Dimension 1 .279 .078 .385
Dimension 2 .238 .057 .282
Dimension 3 .201 .040 .201
Dimension 4 .143 .020 .101
Dimension 5 .079 .006 .031
When a map has low quality – and it is not uncommon to have maps of square tables that explain 20% or less – the map is still showing the strongest patterns evident in the data (i.e., the map is still likely to be useful), but it is likely that some effort will be needed to understand the nature of any patterns that are not evident in the first two dimensions. Some researchers find it useful to create additional charts showing the relationship between the smaller dimensions and three dimensional charts showing the first three dimensions. This can be done by copying the text output into Excel. Often it is more useful to focus on the actual tables of data for additional insights. Although it is common to refer to the proportions of inertia as “proportion of variance” or “proportion of information” explained by the map, it is not strictly accurate. The map only shows relativities and often the most important insights in a table can be found in the row and column totals (i.e., cannot be found using correspondence analysis).
Sometimes, most noticeably in France, the proportions of the first two dimensions are rescaled to add up to 100% (if you ever see a map claiming to show 100%, it is likely that this has occurred). Some researchers show the percentages of each dimension next to the dimension on the map; this only makes sense when the standard coordinates are charted; Q charts the principal coordinates. There are two sets of coordinates that can be used when charting correspondence analysis. The standard coordinates show the position of the brands on the underlying dimensions (i.e., factors). This is analogous to the factors identified in factor analysis. The principal coordinates are the standard coordinates multiplied by the canonical correlations, which causes the dimensions to be on comparable scales. Note, for example, that when we look at Dimension 5 for the standard coordinates, it shows that Pepsi Light is an outlier compared to the other brands, whereas all the values are much closer together when we look at the principal coordinates; this is because dimension 5 is comparatively unimportant (showing only 3.1% of the pattern in the table), and this is reflected in the principal coordinates.
Standard Coordinates: Preferred cola
Dimension 1 Dimension 2 Dimension 3 Dimension 4 Dimension 5
Coca Cola -.92 .31 -.18 -.32 -.41
Diet Coke 1.00 -.94 -2.18 -.57 .86
Coke Zero .35 .36 .08 1.98 .33
Pepsi Light 2.02 -2.78 .61 .41 -4.73
Pepsi Max -.06 -1.41 1.63 -.51 1.18
Pepsi 2.06 1.99 .84 -1.25 -.08
Principal Coordinates: Preferred cola
Dimension 1 Dimension 2 Dimension 3 Dimension 4 Dimension 5
Coca Cola -.26 .07 -.04 -.05 -.03
Diet Coke .28 -.22 -.44 -.08 .07
Coke Zero .10 .09 .02 .28 .03
Pepsi Light .56 -.66 .12 .06 -.37
Pepsi Max -.02 -.34 .33 -.07 .09
Pepsi .58 .47 .17 -.18 -.01
Standard Coordinates: Q3. Age
Dimension 1 Dimension 2 Dimension 3 Dimension 4 Dimension 5
18 to 24 -1.47 .51 .83 -1.46 -.40
25 to 29 -.17 -.46 .37 .85 1.03
30 to 34 -.50 .63 .00 -.23 .77
35 to 39 -.67 .86 -2.01 .23 -.49
40 to 44 1.54 .15 -.93 -1.00 1.54
45 to 49 1.92 2.02 1.38 .47 -1.33
50 to 54 -.55 -.12 .10 1.96 -.04
55 to 64 .27 -1.38 .83 -.28 .02
65 or more .75 -1.71 -1.15 -.45 -2.32
Principal Coordinates: Q3. Age
Dimension 1 Dimension 2 Dimension 3 Dimension 4 Dimension 5
18 to 24 -.41 .12 .17 -.21 -.03
25 to 29 -.05 -.11 .07 .12 .08
30 to 34 -.14 .15 .00 -.03 .06
35 to 39 -.19 .20 -.40 .03 -.04
40 to 44 .43 .04 -.19 -.14 .12
45 to 49 .53 .48 .28 .07 -.10
50 to 54 -.15 -.03 .02 .28 .00
55 to 64 .08 -.33 .17 -.04 .00
65 or more .21 -.41 -.23 -.06 -.18
Example: Correspondence Analysis of Raw Data
Correspondence analysis looks for patterns in the rows and columns of a table. Where the table shows RAW DATA this means that correspondence analysis will focuses on the analysis on identifying differences between respondents. The following technical outputs and Moon Plot show such an analysis.
Total sample
Unweighted
base n = 651
Correspondence Analysis (Traditional)
Inertia(s):
Canonical Correlation Inertia Proportion
Dimension 1 .657 .432 .237
Dimension 2 .650 .422 .232
Dimension 3 .635 .404 .221
Dimension 4 .504 .254 .139
Dimension 5 .446 .199 .109
Dimension 6 .275 .075 .041
Dimension 7 .190 .036 .020
Standard Coordinates: Observations
Dimension 1 Dimension 2 Dimension 3 Dimension 4 Dimension 5 Dimension 6 Dimension 7
1 -.35 -.35 .54 .33 -.64 .10 .34
2 .38 .27 -1.19 -.05 .11 .03 -.04
3 2.82 -.14 -.08 -.30 -.08 .03 .00
4 -.69 2.74 -.70 .18 -.05 -.02 .04
…
650 .92 -.97 -1.43 -.16 .20 .05 -.08
651 -.88 1.11 .53 -2.26 .51 -.07 -.08
Principal Coordinates: Observations
Dimension 1 Dimension 2 Dimension 3 Dimension 4 Dimension 5 Dimension 6 Dimension 7
1 -.23 -.23 .34 .17 -.28 .03 .06
2 .25 .18 -.75 -.02 .05 .01 -.01
3 1.85 -.09 -.05 -.15 -.04 .01 .00
4 -.46 1.78 -.44 .09 -.02 .00 .01
…
650 .61 -.63 -.91 -.08 .09 .01 -.01
651 -.58 .72 .34 -1.14 .23 -.02 -.02
Standard Coordinates: I like them
Dimension 1 Dimension 2 Dimension 3 Dimension 4 Dimension 5 Dimension 6 Dimension 7
AAPT/Cellular One -.50 -.54 .88 .78 -1.67 -3.00 -1.09
New Tel -.52 -.55 .87 .69 -1.54 .48 3.66
One-tel -.53 -.51 .93 .71 -1.85 2.69 -1.91
Optus -.46 1.78 -.44 .09 -.02 .00 .01
Orange (Hutchison) -.71 -.34 1.12 -2.37 .48 -.03 -.04
Telstra (Mobile Net) -.64 -1.16 -1.76 -.01 .21 .02 -.03
Virgin Mobile -.35 -.40 1.21 1.59 2.15 .07 -.08
Vodafone 1.85 -.09 -.05 -.15 -.04 .01 .00
Principal Coordinates: I like them
Dimension 1 Dimension 2 Dimension 3 Dimension 4 Dimension 5 Dimension 6 Dimension 7
AAPT/Cellular One -.33 -.35 .56 .40 -.74 -.82 -.21
New Tel -.34 -.36 .55 .35 -.69 .13 .70
One-tel -.35 -.33 .59 .36 -.83 .74 -.36
Optus -.30 1.16 -.28 .05 -.01 .00 .00
Orange (Hutchison) -.46 -.22 .71 -1.19 .21 -.01 -.01
Telstra (Mobile Net) -.42 -.75 -1.12 -.01 .10 .01 -.01
Virgin Mobile -.23 -.26 .77 .80 .96 .02 -.01
Vodafone 1.22 -.06 -.03 -.08 -.02 .00 .00
Note that now the first dimension explaining 23.7% of the inertia. Coordinates are computed for every respondent; in the output below, most respondents data has not been shown. This approach permits us to chart each respondent’s position on the map; although often these maps are not so useful, as many respondents are on the same position.