Testing the Complement of a Cell
| Related Online Training modules | |
|---|---|
| Automatic Tests Of Statistical Significance | |
| Generally it is best to access online training from within Q by selecting Help > Online Training |
(Beginning in Q5.14.1.0, Cell Comparisons/Compliment testing is now called Exception testing)
The standard significance tests presented in the cells on each table, which are shown by Font Color and Arrows, are computed by first constructing a small table and then computing the test statistics using that small table.
Proportions
Where the crosstab involves two categorical questions, a two-by-two table is constructed using the complements to the shown categories. For example, if looking at a crosstab of age by gender (two categorical questions), the test in the cell showing Males aged 18 to 24, then the test is performed on a table containing four cells:
| Male | Not Male | |
| 18 to 24 | Cell 1 | Cell 3 |
| Not 18 to 24 | Cell 2 | Cell 4 |
Averages
Where the crosstab involves a numeric variable and categorical question, a one-by-two table is constructed using the complements of the categories. For example, if the cell shows Number of Phone Calls of people aged 18 to 24, then the test is performed on the table containing two cells:
| 18 to 24 | Not 18 to 24 | |
| Number of Phone Calls | Cell 1 | Cell 2 |
Example
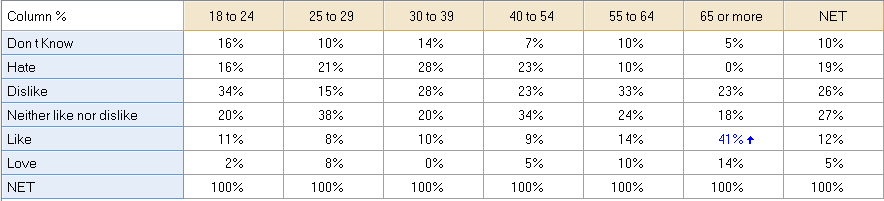
The table below shows a crosstab of two Pick One questions. It shows that people aged 65 or more are more likely to have said they Like the brand (Pepsi Light). Commonly when such significance tests are explained to people it is explained that the 41% is being compared to the total (in this case 12%). That is, it might be explained that “People aged 65 or more are likely to ‘Like’ the brand than the total market.” A more precise explanation is that “People aged 65 or more are more likely to ‘Like’ the brand than people who are not aged 65 or more”. The upwards pointing arrow indicates that the 41% result is higher than what would be expected if there was no relationship between being aged 65 or more and the liking of the brand.
The table below collapses all the categories other than Like and 65 or more collapsed. When Q tests the statistical significance of the 41% shown in this table, the null hypothesis is that sampling error explains the difference between this number and the 10% (i.e., that people aged 65 or more are no more or less likely to Like the brand than people not aged 65 or more). The test used to highlight the 41% on this table is precisely the same test as used in the table above (i.e., when creating Figure 1 Q automatically created lots of these smaller tests in the background and uses these to compute significance. However, when using Multiple Comparison Corrections it is possible to get situations where the collapsed table will have a cell marked as significant and the non-collapsed table will not (and vice versa).
See also
A more technical explanation on Crosstabs of Proportions (One Categorical Question by Another Categorical Question))