Test - Chi-Square Test of Independence

Tests for independence between a pair of categorical variables. Any non-categorical variables that are supplied will be treated as categorical, that is to say, cases with the same value are treated as being in the same category, and date variables are categorised by period.

How to run this test

1. Select Anything > Advanced Analysis > Test > Chi-Square Test of IndependenceCreate > Test > Chi-Square Test of Independence.
2. Specify the variables to use under Inputs > Variable 1 and Inputs > Variable 2
3. Adjust the options (noted below)

You should use numeric variables as inputs. If you use categorical or ordinal variables, they will be coerced to numeric based on their values for the purposes of runnning the test.

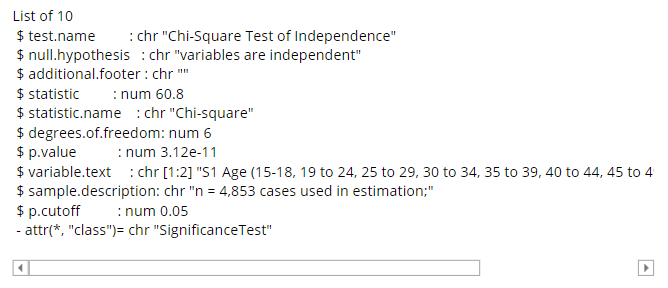
Example

An example output is shown below:

Options

Variable 1 Sample to analyse.

Variable 2 Second sample to compare to Variable 1.

Variable names Display Variable Names in the output, instead of Variable Labels.

More decimal places Display numeric values with 8 decimal places.

Additional Properties

When using this feature you can obtain additional information that is stored by the R code which produces the output.

1. To do so, select Create > R Output.
2. In the R CODE, paste: item = YourReferenceName
3. Replace YourReferenceName with the name of your item. (eg: 'chi_square.test'). You can find this by selecting the item and then going to Properties > General > Name from the object inspector on the right.
4. Below the first line of code, you can paste in snippets from below or type in str(item) to see a list of available information.

Technical details

When no weights are used, the standard Pearson Chi-Square Test of Independence is used.

When weights are used, we use the Second Order Rao-Scott Test of Independence instead of the standard Chi squared test. In this test, the Chi-Square statistic is computed using the weighted counts and then adjusts it using a multiplier that measures the weighted design effect. This weighted design effect involves computing the ratio of the variability with design weights against the variability with simple random sampling. This adjusted statistic uses the F-distribution to compute p-values to account for the extra variability in using the adjustment. It is also named the second order adjustment since the adjusted statistic has the first two moments matched against the asymptotic Chi-Square distribution.

Code

var heading_text = "Chi-Square Test of Independence";
var plural_heading = heading_text.replace("Test", "Tests");
if (!!form.setObjectInspectorTitle)
    form.setObjectInspectorTitle(heading_text, plural_heading);
else
    form.setHeading(heading_text);
form.dropBox({label: "Variable 1",
              types:["Variable: Numeric, Categorical, OrderedCategorical, Text, Date, Money"],
              name: "formVariable1", prompt: "Select the Variable containing the first sample"});
form.dropBox({label: "Variable 2",
              types:["Variable: Numeric, Categorical, OrderedCategorical, Text, Date, Money"],
              name: "formVariable2", prompt: "Select the Variable containing the second sample"});
form.checkBox({label: "Variable names", name: "formNames", default_value: false,
               prompt: "Display names instead of labels"});
form.checkBox({label: "More decimal places", name: "formDecimals", default_value: false,
               prompt: "Display numeric values with eight decimal places"});

library(flipCHAID)
library(flipFormat)
library(flipTransformations)

if (length(formVariable1) != length(formVariable2))
    stop("Variables 1 and 2 have different lengths. ",
         "Please ensure that the variables are from the same data set or have the same length.")

dat.raw <- ProcessQVariables(data.frame(var1 = formVariable1, var2 = formVariable2, stringsAsFactors = FALSE))
dat <- dat.raw[QFilter, ]
dat$var1 <- factor(dat$var1)
dat$var2 <- factor(dat$var2)

weighted <- !is.null(QCalibratedWeight)
svy.weights <- if (weighted) QCalibratedWeight[QFilter]
decimal.places <- if (formDecimals) 8L

appropriateTest <- if (weighted) RaoScottTest else PearsonChiSquareTest
test.args <- list(first.variable = dat[["var1"]], second.variable = dat[["var2"]])
if (weighted)
    test.args <- c(test.args, list(weights = svy.weights))
test.result <- do.call(appropriateTest, test.args)

test.output <- lapply(c("statistic", "parameter", "p.value"), function(x) unname(test.result[[x]][1L]))
names(test.output) <- c("statistic", "df", "p.value")
if (weighted) {
    test.output[["statistic"]] <- setNames(test.output[["statistic"]], "F")
}
SignificanceTest(test.output, "Chi-Square Test of Independence", dat.raw, filter = QFilter,
                 show.labels = !formNames, decimal.places = decimal.places)