Legacy Cluster Analysis
Select Create > Segments > Legacy Cluster Analysis to perform a cluster analysis.
Cluster Analysis forms clusters of similar observations, creating a Pick One question from a Number - Multi question. Q uses k-means cluster analysis. Q uses an expert system to determine the number of clusters; this is useful if you need to prove that the clusters that have been identified are, in some sense, the real and true clusters.
In most instances, Latent Class Analysis should be used instead of cluster analysis, as it takes into account missing data and can appropriately address rankings, categorical data, and experimental data.
Outputs
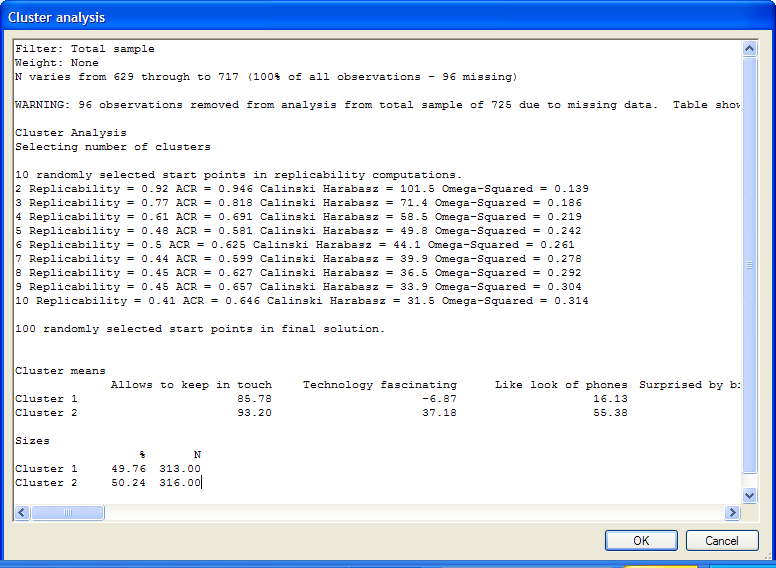
The image below shows the output from a cluster analysis of an attitude battery (Q23 Attitudes from Tutorial 1.Q, with the Question Type changed to Number - Multi question and the values recoded from Strongly Agree to Strongly Disagree as 100, 50, 0, -50 and -100).
The key output from cluster analysis is the Pick One question which is automatically appended to the top of the project file (and shown in the brown drop-down). However, the first output is technical information, which is interpreted as follows:
- The Filter, Weight and sample size are shown at the top of the screen.
- A series of statistics is then presented which are used to select the number of clusters. These statistics are usually computed for between 2 and 10 clusters (and up to 50 if this is warranted).
- The Replicability statistic measures the extent to which the same cluster analysis solution would be identified again if the study was repeated (i.e., if the same questionnaire was administered in the same way to a different sample of people selected in the same manner as the sample being analyzed). A value of 1 indicates that the study would be perfectly replicated and a value of 0 means that it would not likely be replicated at all. Values of 0.8 and above are ‘acceptable’, and values of 0.95 and above are ‘good’. The Replicability statistic will sometimes not be the same if you repeat an analysis – the solution to this is to increase the number of Replications until it is stable.
- The ACR is a penalized version of the Replicability statistic. A method of selecting the number of clusters is to select the number of clusters with the highest value of the ACR.
- The Calinski-Harabasz index (Calinski, R. B. and J. Harabasz (1974). "A dendrite method for cluster analysis." Communications in Statistics 3: 1-27) is another method for selecting the number of clusters. According to this statistic, the higher the number, the more likely the number of clusters is to be correct. Q selects the number of clusters according to whichever is higher of the Calinksi-Harabasz and ACR statistics.
- Omega-Squared is a measure of the proportion of variance accounted for by the cluster solutions (i.e., it is a multivariate version of the R-Squared statistics used in regression).
- Cluster means shows the average values of each of the variables in the question for each cluster. Observations with missing values on one or more of the variables are automatically excluded.
- Sizes refers to the proportion of the sample in each cluster (again, observations with missing values have been filtered out).
- The second last line repeats the omega-Squared figure, expressed as a percentage.
When you press OK, you will see that a table is shown where the rows represent the question that you used in your cluster analysis and the columns represent clusters (i.e., the question in the brown dropdown is a Pick One question representing cluster membership). This table corresponds to the Cluster means table described above. However, in this instance it is based on all the data (irrespective of whether there are missing values or not) and the results may, consequently, differ from those in the table. As with any tables shown on the Outputs Tab, we can rename, drag, drop, sort, etc.
See also
- How to Scale Variables to have a Unit Range
- How to Scale Respondents to have a Mean of 0 and a Standard Deviation of 1
- The following pages on SurveyAnalysis.org
Buttons, options and fields
Number of clusters The number of clusters may be user-defined or computed automatically (using Calinski and Harabasz’s heuristic). Automatic cluster selection will always result in two or more clusters. This should not be interpreted as meaning that there is evidence that the clusters “exist” – cluster analysis is predicated on the assumption that clusters exist.
Maximum iterations The maximum number of iterations of the k-means algorithm. (See Hartigan, J. A. and M. A. Wong (1979). "A K-means Clustering Algorithm." Applied Statistics 28(1): 100-108. If you receive a warning message WARNING: Maximum number of iterations exceeded you should increase this number (e.g., to 1000).
Start points The k-means algorithm is repeatedly run with different randomly selected start points (to reduce the likelihood of identifying a local optima). The Hartigan-Wong clustering algorithm starts with randomly selected cluster centers and re-allocates respondents between clusters so as to maximize omega-squared. Q repeats this process multiple times, selecting the solution with the highest omega-squared.
If Q is automatically selecting the number of clusters, the specified number of Start points are used to conduct the various cluster analyses in each replication and for each number of clusters. However, when the number of clusters is being automatically determined, the number of start points used to generate the final solution is whichever is higher of 100 and the number shown. As a result of this, in some instances the variance percentage shown at the bottom of the outputs may be higher than the number shown in the table.
Increasing the number of start points increases the time taken to conduct the cluster analysis (in the same manner as with increasing the number of replications).
Ignore NET and SUM Excludes the NET or SUM row from the analysis.
Replications Number of replications used when validating the cluster analysis solution. A synthetic sample is constructed by random sampling with replacement from the actual data. Cluster solutions identified in these synthetic samples are then compared to the cluster analysis of the real data using the adjusted rand statistic (Hubert, L. J. and P. Arabie (1985). "Comparing Partitions." Journal of Classification 2: 193-218). The number of Replications is the number of times synthetic samples are generated. The average adjusted rand is then the Replicability statistic.
The default number of replications has been set at 20. This is a comparatively small number and, if the Replicability statistic is of particular interest, it may be useful to use a larger number (e.g., as high as 1000). The time taken for the cluster analysis is a multiple of the number of replications (e.g., if you change the number of replications from 20 to 200 then the cluster analysis will take 10 times as long)